Signifikanztest für Kreuzkorrelationen (»cross-lagged panel correlations«)
(nach D.A. Kenny, 1975)
Downloads
Neben der Javascript-Version dieses Tests (siehe unten) gibt es dieses Programm auch zum Download als
DOS Software - Deutsche Version - (29 KByte)
- DOS Software - English version (29 KByte). Many thanks to Wakefield Carter (email: wake[at]2000ad.nu) who has done the translation.
- Excel Version - (34 KByte)
Beschreibung
Das folgende Javascript prüft zwei längsschnittliche Pearson-Korrelationskoeffizienten, sog. "lagged correlations" (Kreuzkorrelationen) auf signifikanten Unterschied. Ziel ist es eine Entscheidung über die Richtung eines Zusammenhangs zu treffen: Beeinflußt X -> Y oder ist es vielmehr anders herum? Dazu werden die beiden Korrelation rx(t1) y(t2) und ry(t1) x(t2) nach einem von Kenny (1975, siehe auch Kenny, 1973; Kenny & Harackiewicz, 1979) beschriebenen Testverfahren auf signifikanten Unterschied geprüft. Das Programm benötigt als Input lediglich die beiden berechneten längsschnittlichen Vorhersagekorrelationen, die Synchron-Korrelationen (das sind die querschnittlichen Korrelationen zu Welle 1 und Welle 2 zwischen X und Y) und die Stabilitäten von X und Y (Korrelation von Welle 1 mit Welle 2). Außerdem muß noch die Anzahl der Untersuchungsteilnehmer eingegeben werden.
Das Programm prüft auch eine Vorausetzung für die Durchführung des Verfahrens: die Stationarität der Synchronkorrelationen (Kenny & Harackiewicz, 1979). Die Querschnittskorrelationen von X und Y dürfen zu Welle 1 und Welle 2 nicht verschieden hoch ausfallen. Kenny und Harackiewicz (1979, S. 373) unterscheiden neben der "perfekten Stationarität" - die dieses Programm prüft - zwei weitere Formen der Stationarität: Quasi-Stationarität und proportionale Stationarität. Quasi-Stationarität besteht dann, wenn nach der Korrektur der Variablen um Meßfehler (Reliabilitätkorrektur) keine Unterschiede in den Synchronkorrelationen bestehen. In diesem Fall muß vor der Nutzung des Programms eine Reliabilitätkorrektur vorgenommen werden. Dies ist natürlich nur möglich, wenn Informationen über die Reliabilität der Variablen verfügbar sind. Die Minderungskorrektur ergibt sich dann nach Fricke und Treinies (1985, S. 130f) als
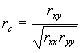
rc = minderungskorrigierte Korrelation; Korrelation
zwischen den "wahren" Werten
rxy = beobachtbare Korrelation
rxx = Reliabilitätskoeffizient für X-Variable
ryy = Reliabilitätskoeffizient für Y-Variable
Den Fall einer proportionalen Stationarität ist nach Kenny und Harackiewicz (1979, S. 373) empirisch in der Regel nicht zu bestimmen, da hierfür mehr als nur zwei Meßzeitpunkte vorliegen müßten. Sollten Stationaritätsprobleme nicht ausgeräumt werden können, bleibt nur der Weg die Cross-lagged Korrelationen mit Hilfe von Strukturgleichungsmodellen auf signifikanten Unterschied zu prüfen (Jöreskog & Sörbom, 1996).
Dieses Skript gibt es auch als Programm unter DOS (ab Version 3.3) und bietet dort eine einfache Eingabemaske für die Korrelationen an. Die Ergebnisse können auch gedruckt werden. Möglicherweise gibt es hier aber mit dem ein oder anderen Drucker Probleme, obwohl nur Standard-Druckerbefehle verwendet werden - NEC P6 und kompatible Nadeldrucker sowie HP Laser- und Tintenstrahldrucker sollten auf jeden Fall funktionieren. Soweit ich das prüfen konnte läuft das DOS Programm in den Shells von OS/2-Warp 3, MS-Windows 3.11 und Windows 95/98/NT und auch innerhalb von DOS Emulatoren auf Linux-Systemen. Die Software ist Freeware, d.h. sie kostet natürlich nichts und kann an jeden Menschen (besser: Computer) weitergegeben werden. Achja, bitte keine Anfragen nach Änderungen oder Quellcode für das DOS Programm - den habe ich leider schon 1990 irgendwohin verschludert.
Bekannte Fehler
Haben beide LAG-Korrelationen - r(X,Y2) r(Y,X2) - ein negatives Vorzeichen, so behauptet das Programm die numerisch höhere Korrelation sei signifikant kleiner als die numerisch kleinere Korrelation (sofern diese überhaupt als statistisch unterschiedlich beurteilt werden). Dies ist natürlich Unsinn und müßte korrekt im Output genau umgekehrt ausgegeben werden.
Fragen und Antworten
Frage: Wo ist nachzulesen, daß Kenny zur Prüfung der
Quasi-Stationarität ein Alpha von .25 vorschlägt?
Antwort: Korrekt! Das steht tatsächlich nicht bei Kenny. Hier geht es
vielmehr um grundlegende Annahmen und Verfahrensweisen, wenn es gilt statistische
Entscheidungen zu fällen. Um es kurz für den vorliegenden Fall auszuführen:
H0: Es besteht kein Unterschied zwischen den Synchronkorrelationen
H1: Es besteht ein Unterschied zwischen den Synchronkorrelationen
Ziel: Ich will H0 beibehalten, also gilt es den Beta-Fehler
möglichst klein zu halten. Der Beta-Fehler wäre der Fehler den wir machen, wenn wir H0
beibehalten, obwohl H1 richtig ist.
Da wir den Beta-Fehler bei unspezifischen Alternativhypothesen (wie in unserem Fall der
Prüfung der Stationarität) nicht direkt bestimmen können, müssen wir uns damit
begnügen den Beta-Fehler indirekt klein zu halten, indem wir den Alpha-Fehler möglichst
vergrößern. Als Konvention hat sich hier ein Alpha von .25 etabliert. Um Bortz (1977, S.
193) zu zitieren: "Entscheiden wir uns bei einem Alpha = 25 % Niveau für H0,
wird diese Entscheidung mit einem kleineren Beta-Fehler versehen sein, als wenn wir bei
einem Alpha = 5% die H0 beibehalten". Jetzt schreib mir bloß keiner,
ich soll mir mal ne neue Auflage vom Bortz kaufen ;-)
Formeln
Damit Sie gegebenenfalls überprüfen können, daß das Programm tatsächlich korrekt funktioniert. Hier noch die Formeln wie sie bei Kenny (1975, S. 896) angegeben sind:
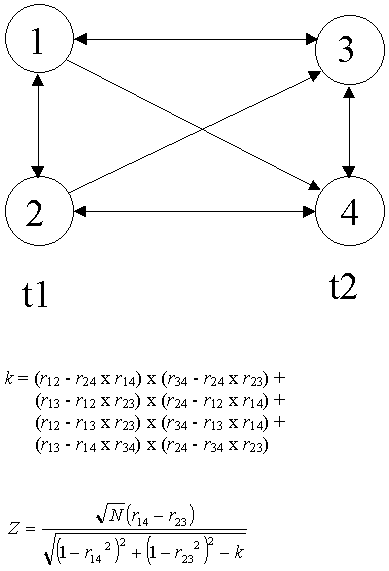
Anmerkung: Die Prüfung der Quasi-Stationarität wird nach der gleichen Formeln berechnet. Allerdings werden hier bei der Prüfgröße Z statt der Lagged-Correlations die Querschnitts-Korrelationen eingesetzt.
Literatur
Bortz, J. (1977). Lehrbuch der Statistik für Sozialwissenschaftler. Berlin: Springer.
Fricke, R. & Treinies, G. (1995). Einführung in die Metaanalyse. Bern: Hans Huber Verlag.
Jöreskog, K.G. & Sörbom, D. (1996). LISREL 8 User's Reference Guide. Chicago: Scientific Software International.
Jöreskog, K.G., Sörbom, D. Toit, S. & Toit, M. (1999). LISREL 8: New Statistical features. Chicago, IL: Scientific Software International.
Kenny, D.A. (1975). Cross-lagged panel correlation: A test for spuriousness. Psychological Bulletin, 82, 887-903.
Kenny, D.A. (1973). Cross-lagged and synchronous comman factors in panel data. In A.S. Goldberger & O.D. Duncan (Eds.), Structual equations in social sciences. New York: Seminar Press.
Kenny, D.A. & Harackiewicz, J.M. (1979). Cross-lagged panel correlation: Practice and promise. Journal of Applied Psychology, 64(4), 372-379.